This post applies if your grid to ground conversion requires needing to apply a horizontal rotation about an origin point and is defined by:
- Horizontal Translation North (tN)
- Horizontal Translation East (tE)
- Horizontal Rotation (Rz)
- Horizontal Origin Northing (N0)
- Horizontal Origin Easting (E0)
- Horizontal Scale Factor
Then, if the horizontal scale factor is one, luckily, the horizontal rotation simplifies things a little as it becomes a translation to the origin, a rotation about the Z axis, translation back, (see figure 1) and then apply the easting and northing translations, if applicable. This would can be done in four applications of the Affine Transform LAS PCT, but it can also be simplified with a little re-factor work ahead of time.
Background Math
We start with the origin point of rotation:
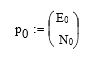
And horizontal translations:
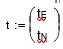
Consider the translation and rotation(z) matrices in figure 1. Then the output, out1, of a point, P1, with an origin of rotation at P0, is given by:
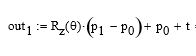
Re-factor the above so a single offset can be used. Where:
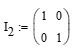
then,
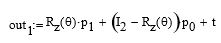
and the constant offset portion is then
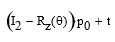
then the single translation values become,
Tx = E0 * ( 1 – cos(Rz) ) + N0 * sin(Rz) + tE Ty = N0 * ( 1 – cos(Rz) ) - E0 * sin(Rz) + tN
In the Affine Transform LAS PCT:
From your inputs,
Compute the value for the horizontal rotation (Rz), if the rotation is given in D°M’SS.SSSS”, then Rz = D + M/60 + SS.SSSS/3600
And singular translation values using the re-factored formulas:
Tx = E0 * ( 1 – cos(Rz) ) + N0 * sin(Rz) + tE Ty = N0 * ( 1 – cos(Rz) ) - E0 * sin(Rz) + tN
- Check the Rotate box
- Enter the value for the Horizontal Rotation (Rz) in decimal degrees
- Check the Translate box
- Enter the value Tx for Translate X
- Enter the value Ty for Translate Y
Cheat Sheet
Use the following spreadsheet to help you quickly compute the values to enter into the LP360 Affine Transform LAS PCT to apply a horizontal rotation about an origin point: