When you ask the question “LIDAR or dense image matching?” with respect to high accuracy drone mapping, you will most likely get an emphatic vote for LIDAR from companies who own a LIDAR and a long list of reasons that LIDAR is bad from those who do not! Obviously, this is not very useful. In this first of a two-part series, I am going to present some information that will allow you to make an informed choice. This first part will focus on systems with precision having a standard deviation greater than 2.5 cm. These systems typically use LIDAR scanners originally designed for automotive applications and typically cost less than US $100,000. I will term these Low Precision LIDAR (LPL) systems. The second half of the article (which I intend to publish in a few months) will focus on scanners with precision better than 2.5 cm (and typically much better) that are purposely built for aerial (and mobile) high accuracy scanning. These systems are typically above US $100,000 in cost. I will refer to these systems as High Precision LIDAR (HPL). GeoCue/AirGon own or have owned both types of systems and thus this article is based on direct observation and experimentation.
First, a bit of background. I use the term “mapping” in a generic sort of way to talk about sensor and geomorphic data used in some sort of modeling. I try not to make artificial distinctions about “survey grade” or “mapping grade” since these terms are not universally defined. I always think in terms of the accuracy requirements of products rather than the methods used to create those products; you can make some really bad products with “survey grade” gear without a whole lot of effort!
The data needed for modeling or analytic analysis from drone mapping generally include an orthophoto and a three-dimensional (3D) point cloud. In the beginning of the drone mapping age (Circa a few years ago!), the only choice for the point cloud was from a camera whose image data are post-processed via dense image matching (or Structure from Motion, SfM) into a point cloud and orthophoto. In the last few years, LIDAR sensors have become compact and light enough to be deployed on moderate size drones such as the DJI m600. This has made point clouds from LIDAR available to drone mappers. If you need an orthophoto (and most customers do want this), you will need to either make two flights over the project area (one with LIDAR and one with camera) or add a camera to your LIDAR mapper.
If you are contracting for drone mapping, you will notice that pricing for a LIDAR project is considerably more expensive than for a camera. In fact, many LIDAR service providers have taken to providing services at a daily rate (typically around $6,000/day) rather than providing firm fixed pricing. This increased pricing is needed because LIDAR equipment is often in the 100K+ price range and LIDAR data collection is considerably more involved than collecting data with a camera. A very good camera-based mapping system with direct geopositioning will cost about 20K (you can buy a full Inspire 2 kit with Loki and full processing software from us for about this amount). If we consider the effective life of a drone mapping system to be 24 months, then amortization of a $100,000 LIDAR system is about $4,167 per month. For the camera-based system, it is about $833 per month. I will talk about the differences in flying later in this article.
I always encourage clients (whether end users who will be collecting their own data or service providers who do the collecting for the ultimate end user) to think in terms of the products that are to be produced, not the data acquisition. It is the Products that will drive the sort of technology that is needed for data acquisition, not the other way around. For example, 1-foot contours require about 1/3 foot network vertical accuracy, a pretty tight specification. Relative volumetrics where no a priori toes or bottom data are being used require only good local accuracy. So products drive technology, not the other way around.
I am not going to go into a treatise on accuracy in this article since this is a very detailed subject in and of itself (I have published a number of articles on this subject in LIDAR Magazine). That said, your concerns around accuracy should include:
- Network Accuracy – this is how well your data fit a geodetic network. It is often mistakenly called “absolute” accuracy. It is typically measured by comparing your collected data to a set of independently located check points where these check points have been tied into a geodetic network.
- Local accuracy – this is how well your data model fits the imaged area in a metric sense. It generally means how well an object of known length or area in your project will be measured in your data (e.g. if you place a rod of exactly 2 meters in length in your project, does it measure 2 meters in your data?). You can have very good local accuracy yet very poor network accuracy but for some projects, this is all that is needed.
- Precision – This is often called “noise.” It is the measure of the spread of data when repeatedly measuring the same areas of a hard surface from the same observation point. For example, if you examine the roof of a perfectly smooth building, by how much do your 3D points deviate from the planar surface defined by the roof?
The final consideration is resolution. Resolution is simply the post spacing of the data in the 3D cloud (the Nominal Point Spacing, NPS) or the spacing of pixels in a digital orthophoto (the Ground Sample Distance, GSD). For example, an ortho with 2 cm GSD is higher in resolution that an ortho with 4 cm GSD. I separate resolution from accuracy since it is a measure of a different property that is not directly related to accuracy. For example, it is easily possible to have data with a resolution of 1 m whose network accuracy is much higher than data with a resolution of 10 cm (think control points, for example).
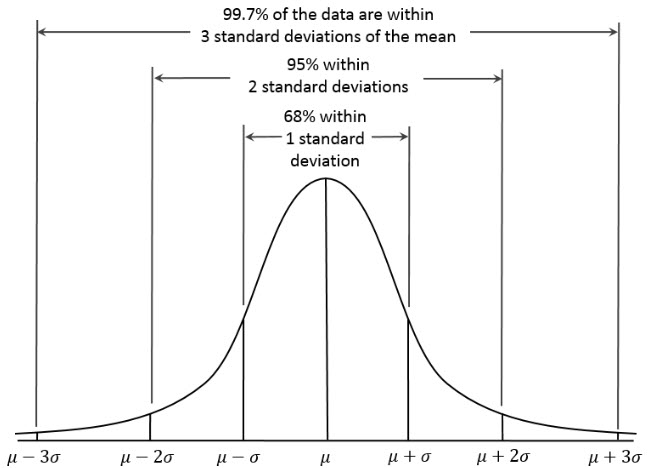
There is an additional consideration that appears with airborne mapping – how well are various surfaces being covered by the mapping data. An example is the density of ground points in areas of tree canopy. I’ll call this effective resolution. To give you an idea of what I mean, consider Figure 1. This is a treed area of our test site modeled using dense image matching. If you consider the ground level (at about 209 m), you see that we have coverage to the left and just a bit slightly to the right of the first clump of vegetation as you move left to right along the profile. The effective ground resolution in these data are very poor in the vegetated areas.
Figure 1: Tree area in SfM data
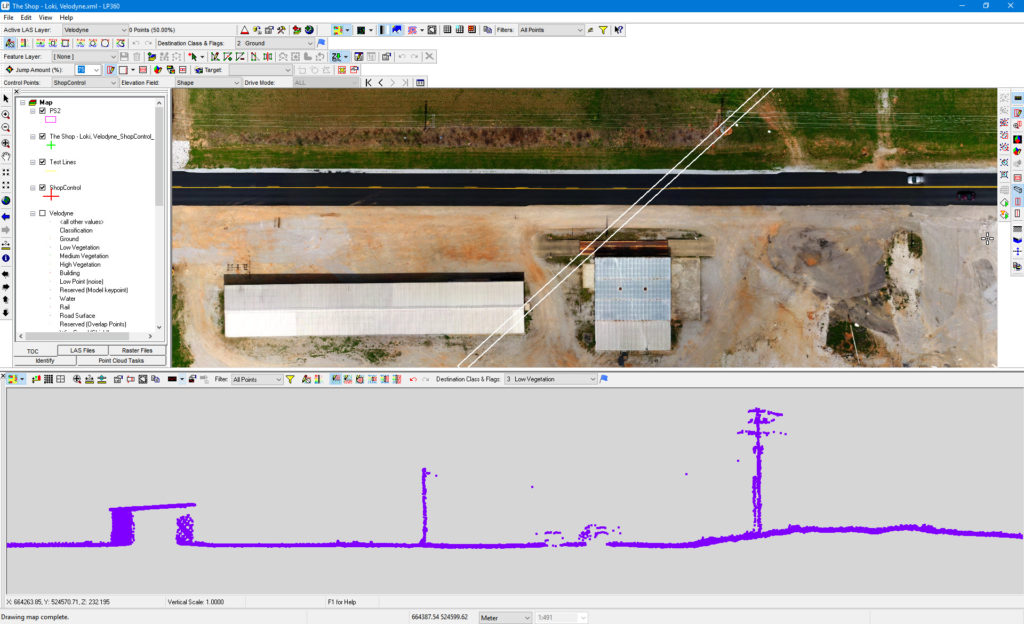
Now consider the image of Figure 2. This depicts the exact same scene using a low precision drone-borne LIDAR (an LPL system). Notice that the resolution of the trees is much improved, and we do see a few scattered ground points throughout the tree line. The effective ground resolution is higher than in the SfM data (but still disappointingly low – more on this later). Of course, those of you who routinely do airborne LIDAR data collection/processing are keenly aware of this distinction. QL-2 LIDAR data is all about having 2 points/m2 in the ground class, not simply in all classes! So, with this terminology in place to reinforce our discussion, let’s move on to the subject at hand – LIDAR versus SfM.
Figure 2: Tree area in LIDAR data
In my opinion, the question is not really LIDAR versus SfM but rather “when is it a good idea to supplement SfM with LIDAR?” In other words, I think you should always do a flight with a camera and then consider if the data need to be supplemented by LIDAR. This means that if you have a drone-based LIDAR, you should either have a camera on the same platform or have a separate system you use for SfM. There are three primary reasons I make this recommendation. The first and most important issue is the limited range of a drone-based LIDAR system’s laser. For example, the practical range of LPL sensors is about 50 meters. If the vertical extent of the project site (that is, the range from minimum to maximum elevation) exceeds about 25 m, you will need to use a terrain following mission plan. You cannot really use stock elevation such as that from Google Earth for mission planning since it is not temporally up to date and additionally will not have the level of accuracy or detail that you need for flying a drone in terrain following mode. You can create the necessary terrain model for mission control by first flying with a camera-based system (which is not nearly so range dependent) and using the SfM generated point cloud to create a digital surface model (DSM).
The second is the number of missions required to cover the project area. Since you will generally be flying the LIDAR system “on the deck”, more flight lines are required. You can save a lot of time by simply supplementing areas of the project where SfM is not adequate rather than flying the entire project with LIDAR.
The final reason is a to provide a partially independent source for checking accuracy. A pet peeve of mine is that many users of LIDAR check vertical accuracy but not horizontal. It is very difficult to check network horizontal accuracy with LPL systems since these sensors tend to have poor fidelity of the pulse return (“echo”) intensity. In Figure 3 is depicted point cloud from an LPL (rendered as a Triangulated Irregular Network, TIN) over a survey check point target. The surveyed location of the check point is indicated by the green cross. There is simply not enough dynamic range in the return pulse intensity of the LPL data to identify the check point. Horizontal accuracy of the LIDAR data can be measured by transferring check points from the SfM data to points within the LIDAR data that are geometrically evident (e.g. vertical edges) rather than trying to use a radiometric approach. You will also note that LPL systems are aptly named. The data from Figure 3 are from a flat, hard, even surface. Note the high noise level evident in this TIN.
Figure 3: LPL point cloud over a check point target
If you average out precision error, low cost LIDAR systems can have good vertical network accuracy. In the examples of this article, we flew a low precision LIDAR (LPL) system and an Inspire 2 equipped with our Loki direct geopositioning system. Both systems had been calibrated. We did not use ground control points (GCP) to correct the data in either system. The comparison of network vertical accuracy is shown in Table 1. As you can observe, the SfM data are actually a bit better in terms of network accuracy as compared to the LIDAR data but the difference is probably not statistically significant.
Table 1: Network Vertical Accuracy
| Vertical Metrics | SfM (Loki System) | Low Precision LIDAR |
| Mean Error | 1.9 cm | 1.5 cm |
| Range (peak to peak) | 10.5 cm | 16.6 cm |
| RMSE | 3.8 cm | 5.2 cm |
| Minimum Contour Interval | 12 cm | 16 cm |
Table 2: Network Planimetric Accuracy for SfM system
| Vertical Metrics | SfM (Loki system) |
| Mean Error | 3.9 cm |
| Range (peak to peak) | 5.6 cm |
| RMSE | 4.2 cm |
We did not set up specific targets to measure the horizontal accuracy of the LIDAR data (these tests were aimed at a different set of metrics). However, we can compare the SfM data to the LIDAR data in regions of sharp vertical edges to get a qualitative idea of accuracy. I used the following procedure:
- Classify the roof of the Shop building in the SfM data
- Using the Point Tracing point cloud task in LP360, automatically draw a polygon that circumscribes the building roof data
- Superimpose this polygon over the same roof classified in the LIDAR data
The result of the above process is shown in Figure 4 for the SfM data set. We know, from the tests against check points, that this polygon is within (speaking Root Mean Square Error, RMSE) 4.2 cm of the correct Network value.
Figure 4: Roof line automatically digitized (in LP360) from SfM data
I next superimposed this same polygon (taken to be within 4.2 cm of “truth”) over the LIDAR data. This is shown in Figure 5. You can clearly see in the profile view the misalignment between the two data sets in the Easting direction. When measured, this different is about 43 cm! This is, needless to say, a rather significant horizontal error. There are a number of causes of this type of error such as pitch calibration, errors in antenna offset and so forth. Since our error is in the Easting direction, regardless of flying direction, I suspect someone made an simple error with base station coordinates. We did not investigate this since the purpose of this particular flight was to test some new mission planning software. However, it does point out how critical it is to have a scheme to measure horizontal error in LIDAR data. If you are contracting for this type of data, make sure your vendor carefully spells out how she will measure this metric.
Figure 5: Roof line from SfM data superimposed on LIDAR data
If you are using a low precision LIDAR (LPL) sensor, you are going to have to deal with a fair amount of vertical noise. Low vertical precision means that if you repeatedly measure the same hard surface with the laser, you will get a range of values rather than a single, clean distance. This “sloppiness” in range is primarily caused by jitter in the clock being used to count the round-trip time of flight or, in multiple beam systems, a failure on the vendor’s part to calibrate the individual beams.
The error in range is usually distributed in a Gaussian fashion. LIDAR vendors usually specify this error as the “1 sigma” range precision error (see Figure 6). LPL sensors tend to have a 1 sigma range precision jitter of about 5 cm. For a Gaussian distribution, 99.7% of the data points will be found within 3 standard deviations of the mean which is +/- 3 sigma or a total error range of 6 sigma. This translates to a 30 cm noise band for LPL with 5 cm of 1 sigma range error. Later on we’ll have a look at peak-to-peak noise (Noisepp) for the LPL and observe that it is indeed in this range.
Figure 6: A Gaussian Distribution
Figure 7 shows a concrete pad at our drone test range (the “Shop”). This is a hard surface with less than 1 cm of surface roughness. If you zoom in a bit on this image (Figure 8), you will be able to see that points from the LPL have excursions in elevation ranging from 106 cm to 141 cm (the profile scale has been set to relative mode). This is a whopping 35 cm (as we predicted a few paragraphs ago)! However, this is a bit heuristic, giving us a visual idea of the peak-to-peak error in the hard surface return.
Figure 7: Hard Surface Ground data from LPL
Figure 8: Closer view of LPL precision range
LP360 has a very nice tool designed to measure point cloud range precision. It is a Point Cloud Task (PCT) called Planar Statistics. This PCT computes statistics of the area of the cloud that you designate with the PCT drawing tools (typically a polygonal area). The PCT defines the best fit plane to the data (using an Eigenvector-based algorithm called Principle Point Analysis, PCA) and then provides measures of the best fit plane and the deviation of points from this plane. The plane that is fit by LP360 is not necessarily a horizontal plane but rather the plane that is the best fit to the local area of the point cloud, regardless of slope. This means you can also use the tool to test data on sloped surfaces such as roofs. The metrics of precision are shown in the snippet of Figure 9. Here you can see the standard deviation is 4.66 cm and the range is 33 cm.
Figure 9: LPL hard surface range precision statistics (values in meters)
There is a (unfortunately) widely held myth that LIDAR data provides better vertical accuracy than SfM. This is not true, in general. First of all, a bad sensor is going to give bad data, regardless of the data type (I am not saying the LPL is bad. There are, however, some really bad cameras and really bad LIDAR units out there!). SfM has two major components to the processing chain. The first is block bundle adjustment. Those of you with a photogrammetry background will immediately recognize this as the “Aero Triangulation” or AT step. This part of the flow is used to determine the exact position of the camera with each exposure. This is called the Exterior Orientation, EO. If we precisely know EO and we have carefully calibrated the camera, we can use image overlap to locate points in 3D. Framing cameras (the usual type in drone mapping but make sure you are using one with a mechanical shutter) have very strong geometry and therefore can produce remarkably accurate ray intersections. The second part of SfM is the generation of the dense 3D point cloud using techniques such as semi-global matching (SGM). This second part is the Achilles heel of SfM. In areas of bare earth, the matching is quite good and the resultant point cloud will be clean (high precision) and accurate. However, in areas where all participating images cannot see the object of interest (such as over tree canopy) or the surface exhibits poor texture, the algorithm breaks down. Knowing where this will occur is critical when planning image-based drone mapping projects.
Let’s examine the SfM point cloud over this same concrete apron. We used an Inspire 2 with a laboratory calibrated X4s camera. Our Loki direct geopositioning system was used for determining the X, Y, Z position parameters of the camera station exterior orientation (EO). The data were processed through Agisoft PhotoScan with no ground control. A screen shot of a profile of the SfM data on the apron is shown in Figure 10 (the graticule spacing is 5 cm). The peak to peak noise is about 5 cm. This is nearly an order of magnitude better than the LPL system. In addition, these data were collected at over twice the flying height of the LIDAR.
Figure 10: SfM precision range
If we perform the same quantitative examination using the LP360 Planar Statistics PCT on the SfM data set as we did on the LIDAR, we obtain the results of Figure 11. Note the standard deviation is 1.05 cm and the range (Peak to Peak) is 5.86 cm. This is comparable to a High Precision LIDAR (HPL), the focus of a future article.
Figure 11: SfM hard surface range precision statistics (values in meters)
You can clearly see that in areas of bare earth, SfM from a relatively low-cost camera (the X4s is about $700) is not slightly better than the LPL data but nearly an order of magnitude better!
The question comes to mind “where would we use a low cost LIDAR system such as an LPL?” since modeling bare earth using SfM is clearly better. The answer is, of course, vegetation where a ground model is needed or where we are explicitly trying to model above ground linear features such as power lines. Figure 12 depicts the profile of a vegetated area of the Shop test site using SfM. Note first of all the characteristic below-ground noise (in purple) in the tree area. This is typical of SfM data. It is caused by correlation errors between the overlapping images. When doing automatic ground classification, you must first classify out these low noise areas to prevent them from erroneously seeding the ground algorithm (LP360 has an automatic routine for classifying Low Noise). The second and more important thing to note is the complete lack of any ground points under the tree canopy. When performing SfM photogrammetry, at least three images must see the exact same point on the ground to correlate a match. This geometry is possible in sparse scrub brush but impossible in moderately dense vegetation.
Figure 12: Vegetated area using SfM
Compare this to the LPL data of Figure 13. Note the more detailed rendering of the tree canopy. More importantly, notice that we have several ground points under the tree canopy, something that is not possible with SfM modeling. Finally, notice that we do not see any low noise points under the canopy. We can clearly see, however, the low precision in the LPL data as exhibited by the “fatness” of the ground profile (caused by high peak-to-peak noise) as compared to the SfM rendering of Figure 12.
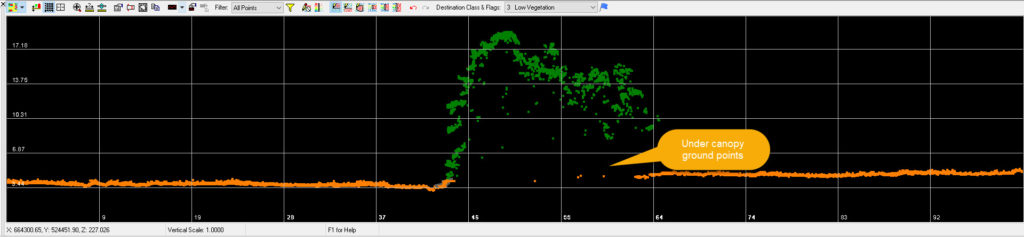Figure 13: Vegetated area using LPL
Let’s have a look at one final type of modeling, that of wires. Figure 14 shows a distribution wire extending from a pole-mounted transformer to the Shop building. Note that we can see the poles as well as a tiny bit of the wire (four points, to be exact). Thus the LPL is providing an idea of the overhead components in this portion of the data. The data are quite fuzzy due to the low precision of the LPL range.
Figure 14: Distribution wire modeled with the LPL point cloud
Figure 15 depicts this same scene modeled with the SfM point cloud. Not only is the wire gone but all of the foreground pole and all but a blobby looking transformer on the far pole are missing. As you can see, nadir collected SfM is entirely unsuited for linear feature extraction. I would argue that the same is true of low precision LIDAR since the model created from the LPL wire points would not adequately represent the true wire geometry.
Figure 15: Distribution wire modeled with the SfM point cloud
So what is the conclusion of all of this? Basically it is to use SfM everywhere except where you can’t. Discuss requirements with your customer (or yourself if you are the customer). Ask if vegetated areas need to be modeled. For example, if you are generating 1-foot contours of an active mine area, are contours needed for the vegetated areas? Unless the mine is horizontally expanding, the answer is usually no; you should either omit these areas in your deliverables or delineate them with polygons indicating low confidence areas. If you are using a LIDAR system with low precision such as an LPL, use SfM everywhere you can and supplement with the LIDAR data in areas where SfM does not work. A note of caution; when fusing data sets you must ensure that they both are accurately aligned with the same Network vertical datum.
The notion that LIDAR is better than SfM is clearly not true in the case of low precision LIDAR (LPL) systems. In my opinion, the precision of these systems is so poor that I would use them only where it is absolutely required. If vertical precision is important (high accuracy topography such as 1-foot contours), I simply would not use a low precision system such as an LPL. If I did not have a high precision LIDAR (HPL) instrument in my sensor portfolio, I would team with a company who does have one.
In a future article, I will repeat the essence of this study but using a HPL. You will be amazed at the difference. In the meantime, mind your precision!
